Determining the hour angle is an essential step in calculating the position of the sun in the sky for solar energy applications. The hour angle defines the time of day in angular units relative to the solar noon position overhead. Calculating the hour angle properly is key to determining the sun’s declination angle and plotting its coordinates in the sky.

In this guide, we explain what exactly the hour angle represents, and its importance in solar position calculations, and provide a step-by-step walkthrough on how to manually calculate the hour angle for a given location and time.

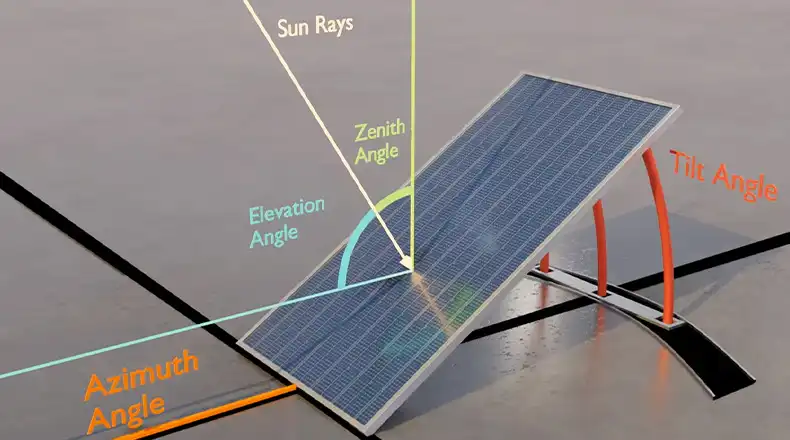
Why Hour Angle is Important

Hour angle is a crucial intermediate value needed to determine the sun’s position in horizontal coordinate calculations or when converting between equatorial and horizon coordinate systems.

By combining the hour angle with the sun’s declination angle, you can mathematically pinpoint the sun’s location in the sky for a given place and time. This allows the proper orientation of solar panels, planning of solar farms, modeling of shadows, and more.

Hour angle also indicates how high the sun will appear in the sky, which impacts solar irradiance and PV system output. Correct hour angle values are the foundation for highly accurate solar position and sun path diagrams.

How to Calculate Hour Angle

Here is the step-by-step process to manually calculate the hour angle at a specific location and time. However, this is a rough calculation for calculating the hour angle. To get the true hour angle, you will need to include the value of the equation of times and the solar declination angle. Here are both calculations are provided. Follow whichever you want –

Rough Calculation 

Step 1. Identify Your Local Time

The first step is to note your local clock time for which you want to determine the hour angle. Be sure to identify your time zone as well.

For example, your time might be 9:30 AM Eastern Standard Time.

Step 2. Convert Local Time to Greenwich Mean Time (GMT)

Next, convert your clock time in your local time zone to the equivalent GMT time. You will need to factor in the offset between your time zone and Greenwich, England.

For most time zones, the offset ranges from UTC-12 to UTC+14 hours. UTC or GMT is the zero reference line.

So for 9:30 AM EST, the time zone offset from GMT is -5 hours. Therefore, 9:30 AM EST becomes 14:30 GMT.

Step 3. Express GMT Time in Decimal Hours

To simplify the calculations, express the GMT time in decimal hours rather than hours and minutes.

Convert the hours to decimals and add the decimal minutes. 14:30 GMT becomes 14.5 hours in decimal format.

Step 4. Subtract 12 Hours from the GMT Time

This step centers the upcoming angles on the Greenwich prime meridian line by moving to a noon reference frame.

For our example, 14.5 hours – 12 hours = 2.5 hours

Step 5. Take the Absolute Value

If the result from step 4 is negative (before solar noon), take the absolute value to remove the negative sign. This yields the final value of the hour angle.

So, the hour angle is = 15° * 2.5 =37.5°

Proper Calculation

we have data on New York City here. So, let’s find out the solar angle now. 

New York City on June 21 at 9:30 AM EDT

Longitude = 74°W

Latitude = 41°N

Step 1. Determine fractional year (γ):

The formula is γ =  2π/365 * [day of year – 1 + {(hour – 12)/24}]

γ = 2π/365 * (172 – 1 + 9.5/24)

γ = 2.4425 radians

Calculate equation of time (eqtime):

eqtime = 229.18*{0.000075 + 0.001868cos(γ) − 0.032077sin(γ) − 0.014615cos(2γ) − 0.040849sin(2γ)}

eqtime = -0.863 minutes

Step 1. Calculate solar declination (δ):

δ = 0.006918 − 0.399912cos(γ) + 0.070257sin(γ) − 0.006758cos(2γ) + 0.000907sin(2γ) − 0.002697cos(3γ) + 0.001418sin(3γ)

δ = 0.40564 radians

Step 2. Determine time offset:

Time offset = eqtime + 4longitude – 60timezone

                  = -0.863 + 4*-74 – 60*-4 = -12.63 minutes

Calculate true solar time:

13:29 GMT

0:12.63 time offset = 13:16.37 True Solar Time

 So, the hour angle will be = 15° * (13.26 – 12) = 18.9°

Bonus Tips – Calculating Azimuth

For calculating the Azimuth angle, you will need to know the latitude(), declination() value, and zenith value. Let’s assume that, the latitude value is 50°, the declination value is 40°, and the time is sunset, so, the zenith(z) value is 90°.

Now, let’s calculate the Azimuth angle’s value.

The formula is, CosA = cos(90-δ) – cos(90+θ)coszsin(90-θ)sinz = cos(90-40) – cos(90+50)cos90sin(90-50)sin90 = 1°

A = cos-1(1) = 0°

Conclusion

Whether you are trying to aim solar panels, model shadow effects, or analyze the optimal siting of a solar farm, determining the sun’s position in the sky is vital. Calculating the hour angle is the necessary first step in this process.

As we have covered, the hour angle represents the angular distance on the earth’s surface between the observer’s meridian and the sun’s position, advancing 15° per hour. By going through the straightforward sequence of time zone conversion, decimalization, and centering on noon, you can accurately find the hour angle for any location and point in time.

Combined with declination, now you have the key inputs to mathematically pinpoint the sun’s celestial coordinates for proper solar calculations. Understanding hour angles unlock the power to harness sunlight across all solar energy applications.